Understanding time and space complexity is crucial for programmers to write efficient code. Time complexity measures how long a program takes to run, while space complexity measures the memory space it uses.
Writing efficient code or inefficient code and somebody who’s aiming to enter into a product based company must always keep this in the back of their mind that it is not about writing code it is always about writing efficient code which takes the least amount of time and least amount of memory to perform its operation now understood why time and space complexity is required let’s begin by laying a solid foundation.
Different approaches to solving a programming problem can have the same output but vary in efficiency, impacting the time taken for execution.
Time Complexity: Time complexity helps programmers estimate how long a program will take to execute by analysing the frequency of statements in the code.
Space Complexity: Space complexity involves analysing the memory space a program consumes during execution, aiding in writing efficient code with minimal memory usage.
Time Complexity:
Understanding time complexity in code involves analyzing how the code’s execution time increases with input size. By using Big O notation, we can simplify the time complexity to the highest order term, like O(n), representing linear time increase.
Different approaches to solving a programming problem can have the same output but vary in efficiency, impacting the time taken for execution.
Time complexity helps programmers estimate how long a program will take to execute by analyzing the frequency of statements in the code.
Time complexity helps us estimate how much longer it will take when input grows.
Example 1: Constant Time → O(1)
func getFirstElement(arr: [Int]) -> Int {
return arr[0]
}- No matter if the array has 10 elements or 1 million, this takes the same time.
- Because we just look at one element.
Complexity: O(1) (constant time)
Example 2: Linear Time → O(n)
func printAll(arr: [Int]) {
for num in arr {
print(num)
}
}- If array has 5 elements → 5 prints
- If array has 1000 elements → 1000 prints
- Time grows directly with input size
Complexity: O(n) (linear time)
Example 3: Quadratic Time → O(n²)
func printPairs(arr: [Int]) {
for i in 0..<arr.count {
for j in 0..<arr.count {
print("(\(arr[i]), \(arr[j]))")
}
}
}
- If array has 5 elements → 25 pairs
- If array has 100 elements → 10,000 pairs
- Time grows much faster as input increases (square growth).
Complexity: O(n²) (quadratic time)
Logarithmic Time → O(log n)
Imagine searching for a word in a dictionary:
- You don’t start from page 1.
- You open the middle, check, then cut half the dictionary and repeat.
func binarySearch(arr: [Int], target: Int) -> Bool {
var left = 0, right = arr.count - 1
while left <= right {
let mid = (left + right) / 2
if arr[mid] == target { return true }
if arr[mid] < target {
left = mid + 1
} else {
right = mid - 1
}
}
return false
}How to calculate time complexity of program ?
Example: Star Pattern
for (int i = 0; i < n; i++) { // Loop 1
for (int j = 0; j < n; j++) { // Loop 2 (nested inside Loop 1)
System.out.print("*"); // Statement A
}
System.out.println(); // Statement B
}
Time complexity calculation
for i in 0..<n → n + 1
for j in 0..<n → n * (n + 1)
print("*") → n * n
print() → n
Total = n+1 + n² + n + n² + n
Conditions:
1. Eliminate Constants
2. Retain the highest ordered term
Constant eliminated that is 1
n + n² + n + n² + n = 3n + 2n²
Eliminate the constants again
n + n²
From n + n² retain the highest order term i.e n²
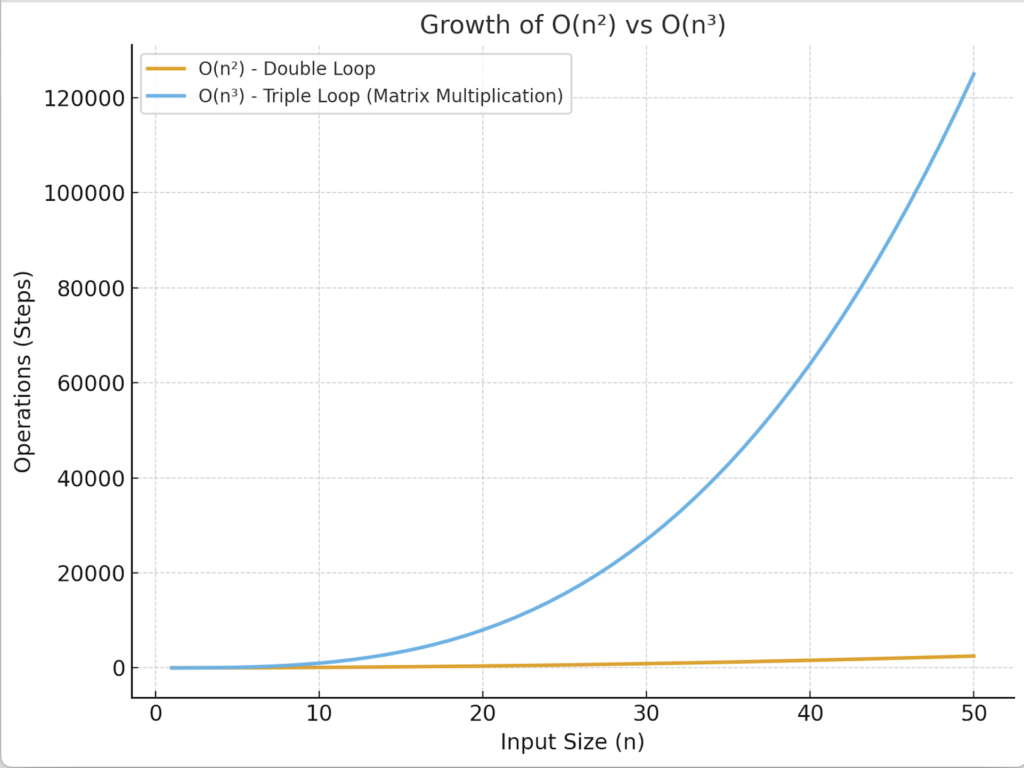
So the final time complexity will be n², it can be represent as O(n²).
Example 2: Matrix Multiplication
func multiplyMatrices(_ A: [[Int]], _ B: [[Int]]) -> [[Int]]? {
let m = A.count // rows in A
let n = A[0].count // cols in A
let nB = B.count // rows in B
let p = B[0].count // cols in B
var C = Array(repeating: Array(repeating: 0, count: p), count: m)
for i in 0..<m {
for j in 0..<p {
for k in 0..<n {
C[i][j] += A[i][k] * B[k][j]
}
}
}
return C
}Calculation of time complexity
for i in 0..<m → n + 1
for j in 0..<p → n * (n + 1)
C[i][j] = 0 → n * n
for k in 0..<n → n * n *(n + 1)
C[i][j] += A[i][k] * B[k][j] → n * n * n
n + 1 + n² + n + n² + n³ + n² + n³
2n + 3n² + 2n³ (Remove All Constants)
n + n² + n³ (Remove lower order terms and preserve higher order term)
n³
Hence time complexity is O(n³)